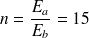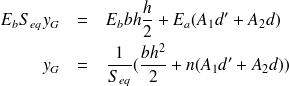Section en Béton Armé
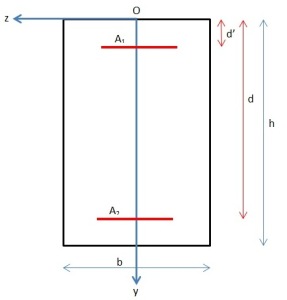
L'objectif de cet exercice est de déterminer les caractéristiques équivalentes d'une section en béton armé, dont vous trouverez la schématisation ci-contre. Afin de rendre un peu plus concret cet exercice, nous allons considérer les dimensions de la section suivantes :
Le rapport des modules d'élasticité
|
Question
Déterminez la section équivalente de béton armé.
Nous considérerons le béton non fissuré
La section d'acier n'est pas ôtée du béton.
Dans un premier temps, établissez un tableau pour récapituler toutes les caractéristiques de chacune des parties de la section.
L'homogénéisation doit se faire par rapport au béton
Nous homogénéisons par rapport au béton.
La section de béton est égale à bh, celle de l'acier est égale à A1+A2
Par conséquent :
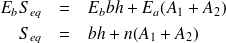
Seq=2442cm2
Question
Question
Déterminez l'inertie de la section Iz
L'inertie propre des aciers sera négligée (c'est pour ça qu'elle ne vous est pas communiquée)
Il n'est pas possible d'additionner les inerties. L'addition des inerties nécessite que ces inerties soient calculées par rapport à un même axe, à un même point. Il faut donc utiliser Huygens pour ramener dans un premier temps l'inertie de chacun des matériaux au centre de gravité précédemment calculé.
Béton :
Inertie propre :
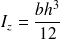
Application de Huygens :
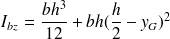
d'où Ibz=63.8dm4
Acier : application directe de Huygens :
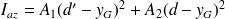
d'où Iaz=4.9dm4
Il est alors possible d'assembler les deux matériaux
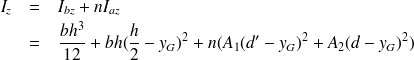
Soit alors Iz = 137,3dm4
Question
Remplissez un tableau récapitulatif
Béton | A1 | A2 | Assemblage | |
|---|---|---|---|---|
n | 1 | 15 | 15 | |
S | 2100 | 3,14 | 19,63 | 2442cm2 |
yG | 30 | 5 | 50 | 31,9cm |
Iz | 63 | - | - | 137,5dm4 |
Huygens | 63.8 | 78.5 10-4 | 4.91 |