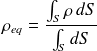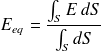Définition "mécanique" des poutres
Les sections ne sont pas uniquement définies en fonction de leur géométrie, mais aussi en fonction des matériaux qui les constituent, et en particulier la masse volumique
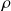et le module d'Young E. De plus, en Génie Civil, plusieurs matériaux aux caractéristiques physiques et mécaniques différentes peuvent être associés, en général le béton et l'acier, que ce soit en béton armé ou en construction mixte.
Les sections ne sont plus alors définies en fonction de leurs caractéristiques géométriques, mais en fonction de ces caractéristiques homogénéisées par rapport à un matériau dont les caractéristiques mécaniques et physiques serviront dans les calculs de RDM.
Les équations de bases restent rigoureusement les mêmes. Seul intervient le paramètre physique
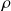ou mécanique E.
Il s'avère nécessaire de définir un matériau de référence, que l'on indicera, dans ce qui suit, 1.
Définition : Section homogénéisée
La section devient une section équivalente définie par :
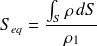, par rapport à la masse
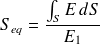, par rapport au module d'Young
Définition : Centre de masse ou centre d'inertie.
Le centre de gravité devient centre de masse ou centre d'inertie, défini par :
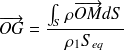pour le centre de masse 
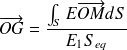pour le centre d'inertie
Définition : Inertie équivalente ou inertie homogénéisée
L'inertie de la section suivant
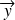tout comme, par analogie, l'inertie suivant
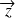, est définie de la même façon que précédemment en ajoutant les caractéristiques physiques ou mécaniques. Le centre de gravité pris en compte est le centre des masses ou le centre d'inertie.
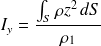pour les caractéristiques physiques
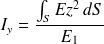pour les caractéristiques mécaniques
Complément : Caractéristiques physiques / mécaniques équivalentes
Il est aussi possible de définir une masse volumique équivalente ou un module d'Young équivalent en écrivant :
Cette méthode est plutôt utilisée lors de la modélisation des éléments.
