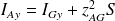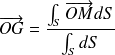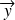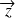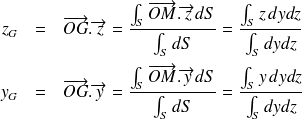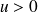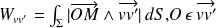Définition géométrique des poutres
Équations de base
Définition : Définition mathématique d'une surface
Une surface est définie comme :
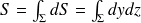
Définition : Centre de gravité ou barycentre
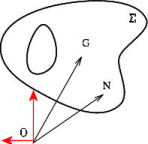 | Soit G le centre de gravité, O un point de repère et M un point quelconque. G est défini par :
En projection sur les axes
|
Définition : Moment statique
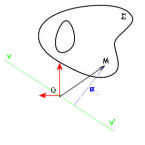 Calcul du moment statique | Le moment statique d'une surface ds par rapport à un axe vv' est défini par le produit u.ds avec
Ainsi, en intégrant sur toute la section, nous pouvons écrire de façon mathématique,
|
Complément : Application à un système d'axe Oyz
Dans le cas d'un système d'axe Oyz, il est possible de définir le moment statique par rapport à ces axes :
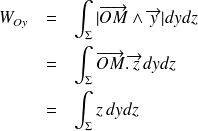
De la même façon
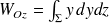
Définition : Moment quadratique et inertie
Le moment quadratique d'une surface S plane par rapport à un axe est la somme des produits des surfaces élémentaires ds infiniment
petites par le carré de leur distance par rapport à cet axe. Par abus de langage, le moment quadratique est appelé inertie ; défini par rapport à un point et un axe, il s'écrit :
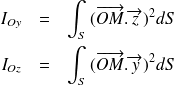
Complément : Inertie
En général, l'inertie est définie au centre de gravité de la section. Les équations sont alors simplifiées :
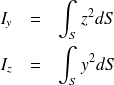
Quelques démonstrations
Relation moment statique - barycentre
Fondamental : Relation moment statique - barycentre
Le moment statique par rapport à un axe passant par le centre de gravité est nul.
Théorème de Huygens
Fondamental : Énoncé du théorème de Huygens