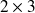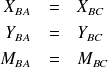Principe Fondamental de la statique - Équilibre des systèmes plus complexes
Problématique
En général, les structures ne sont pas composées de poutres indépendantes, mais plutôt d'un système de poutres assemblées entre elles pour former des portiques.
Les conditions aux limites de ces portiques font que les réactions d'appuis ne peuvent pas être déterminées par un équilibre global du système. Il s'avère alors nécessaire, avant de faire le moindre calcul, de savoir si, dans l'état actuel de nos connaissances, il nous est possible de résoudre le système.
Équilibre des nœuds
Chaque point de la structure se doit d'être en équilibre. Or notre structure est composée de barres et de nœuds, liaisons entre 2 (ou plus) barres.
Ainsi, les nœuds doivent aussi être équilibrés. Nous parlons alors d'équilibre des nœuds.
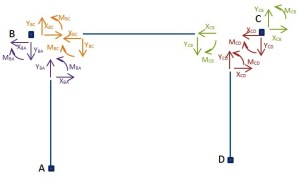
 Schéma d'un portique | Prenons par exemple un portique. Ce portique est composé de 3 éléments barres AB, BC, CD avec des conditions aux limites en A et en D quelconques et un système de chargement quelconque de notre portique. |
Il est alors possible de décomposer la structure en barres et nœuds. A chaque jonction de 2 barres, il est alors possible de définir
Ainsi, au noeud B, nous pouvons écrire :
Ces inconnues sont appelées inconnues de liaison. Par la suite, nous nous réduirons au même schéma, sans passer par l'étape des noeuds, et nous réduirons l'écriture de ces inconnues de liaison à :
|  Schéma d'un portique éclaté |
Complément : Forces aux nœuds
Que se passe-t-il quand une force est directement appliquée à un nœud ?
Degré d'hyperstaticité
b
Complément : Relâchement des nœuds
Un nœud est relâché quand une translation ou une rotation est permise. En général, il s'agit plutôt d'un relâchement en terme de rotation, ce qui signifie que les 2 barres liées peuvent tournées librement l'une par rapport à l'autre. On parle alors de rotule et le moment au nœud est nul. Ceci élimine certes une inconnue de liaison, mais par la même aussi une équation d'équilibre.
En résumé
Améliorons l'algorithme de résolution
Méthode :
Associer à la structure un repère galiléen
Identifier les conditions aux limites
Identifier les réactions aux appuis
Si la structure est un portique
Déterminez le nombre de barres
Déterminez le nombre d'inconnues de liaisons
Calculez le degré d'hyperstatisme
Si
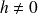nous ne pouvons pas résoudre le systèmeSi h = 0 le système est isostatique
Appliquer le PFS
sur l'ensemble de la structure
éléments par éléments si sur l'ensemble de la structure cela ne suffit pas
